I’ve always wanted a structural diff tool, so I built difftastic.
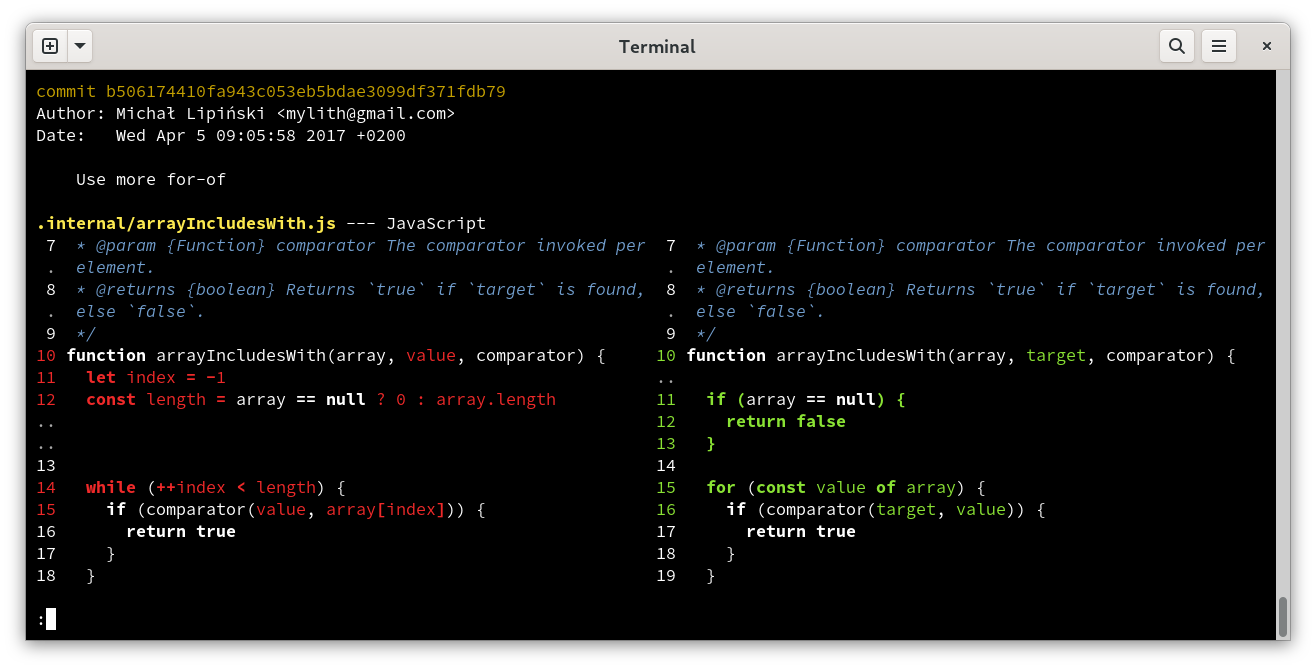
This has been the most fascinating, most frustrating, and most challenging program I’ve ever written.
How Hard Could It Be?
If you write Lisp code for a while, you start to see code like JSON. Everything is basically a list.
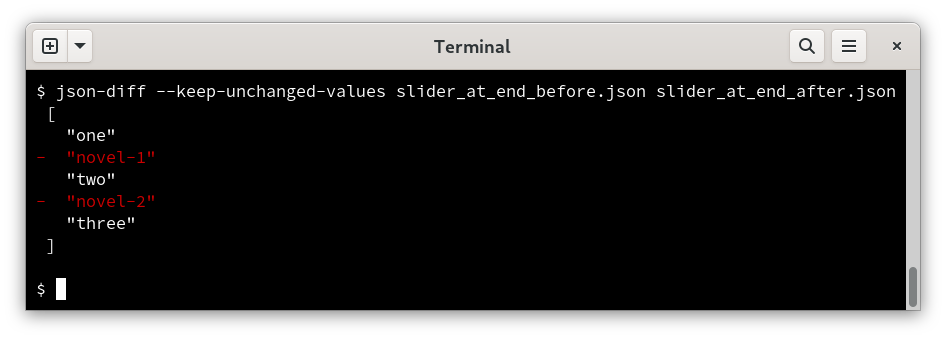
json-diff already exists, and it’s pretty good. I wanted something similar for programming languages.
After a huge amount of experimentation, I have something that works. In this post, I’ll show you how it works.
I won’t show the many, many dead ends and failed designs along the way. We can pretend that I got it right first time.
Parsing The Code
If I want to compare two programs, I first need a parse tree for each program. I need an accurate lexer, a basic parser, and I need to preserve comments.
tree-sitter was a great fit here. You define a grammar in JSON or JS, and it generates a C library that anyone can use. It’s not 100% accurate (e.g. the C++ parser doesn’t have preprocessor data) but it’s more than good enough.
list: ($) => seq("(", repeat($._sexp), ")"),
vector: ($) => seq("[", repeat($._sexp), "]"),
Here’s an excerpt from my Emacs Lisp grammar. There’s a ton of tree-sitter parsers available too. Difftastic now supports 44 different syntaxes, and adding new ones is so straightforward that my manual includes a worked example.
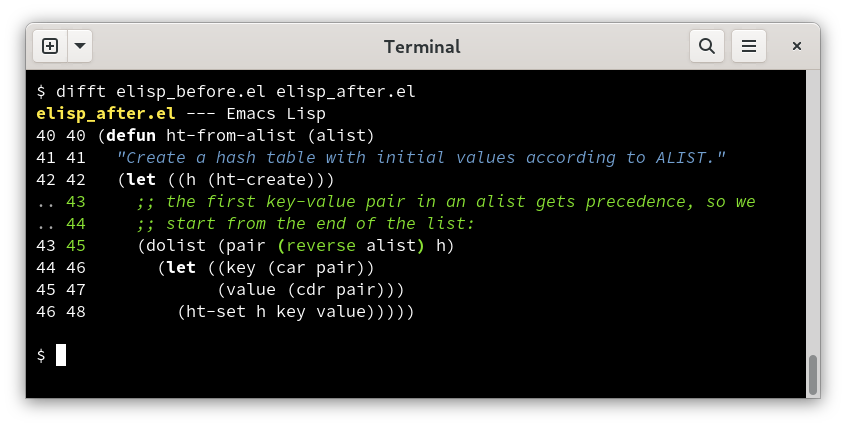
After parsing, difftastic converts the tree-sitter parse tree to an s-expression. Everything is a list or an atom. This uniform representation enables the diffing logic to work on any language that I can parse.
For example, given a JavaScript program like this:
foo(1, 2)
tree-sitter parses it to this parse tree:
expression_statement
call_expression
identifier "foo"
arguments
(
number "1"
,
number "2"
)
difftastic then converts the tree to this s-expression representation:
List {
open_content: "",
children: [
Atom "foo",
List {
open_content: "(",
children: [
Atom "1",
Atom ",",
Atom "2",
],
close_content: ")",
},
],
close_content: "",
}
Calculating The Diff
Fun fact: I thought of diffing programs as working out what has changed. The goal of diffing is actually to work out what hasn’t changed! The more stuff you can match up, the smaller and more readable your diff.
How do I work out what’s changed between two parse trees? There are a bunch of different design ideas out there, but autochrome is the most effective approach I found, and it includes an incredibly helpful worked example.

Autochrome and difftastic represent diffing as a shortest path problem on a directed acyclic graph. A vertex represents a pair of positions: the position in the left-hand side s-expression (before), and the position in the right-hand side s-expression (after).
The goal is to find the shortest route from the start vertex (where both positions are before the first item in the programs) to the end vertex (where both positions are after the last item in the program).
For example, suppose you’re comparing the program A with X A. The
vertices look like this.
START
+---------------------+
| Left: A Right: X A |
| ^ ^ |
+---------------------+
END
+---------------------+
| Left: A Right: X A |
| ^ ^|
+---------------------+
The edges in the graph represent the changes required to transform the left-hand side program into the right-hand side.
In this example, there are two possible changes from the start vertex, so it has two edges. Difftastic could (1) consider the left-hand side to be novel and increment that position, or (2) it could consider the right-hand side to be novel and increment that position.
A novel item on the left-hand side is a removal, and a novel item on the right-hand side is an addition.
START
+---------------------+
| Left: A Right: X A |
| ^ ^ |
+---------------------+
/ \
Novel atom L / \ Novel atom R
1 v 2 v
+---------------------+ +---------------------+
| Left: A Right: X A | | Left: A Right: X A |
| ^ ^ | | ^ ^ |
+---------------------+ +---------------------+
When both positions are pointing to an identical s-expression, a third edge is added in the graph. This edge represents matching an s-expression on both sides.
2
+---------------------+
| Left: A Right: X A |
| ^ ^ |
+---------------------+
/ | \
Novel atom L / | \ Novel atom R
v | v
+---------------------+ | +---------------------+
| Left: A Right: X A | | | Left: A Right: X A |
| ^ ^ | | | ^ ^|
+---------------------+ | +---------------------+
| | |
| Novel atom R | Nodes match | Novel atom L
| | |
| END v |
| +---------------------+ |
+-------->| Left: A Right: X A |<---------+
| ^ ^|
+---------------------+
This ‘unchanged node’ edge has a lower cost than the ‘novel node’ edges. The routing problem is then a matter of finding the route with the most unchanged edges.
The shortest route with programs A and X A is [Novel Right,
Unchanged].
Finding The Shortest Route
Difftastic and Autochrome both use Dijkstra’s algorithm. Unfortunately the size of the graph is quadratic: it’s O(L * R), where L is the number of items in the left-hand s-expression and R is the number of items in the right-hand s-expression.
To make performance bearable, difftastic aggressively discards obviously unchanged s-expressions at the beginning, middle and end of the file. If you’ve only changed the last function in a file, difftastic won’t consider the other functions at all.
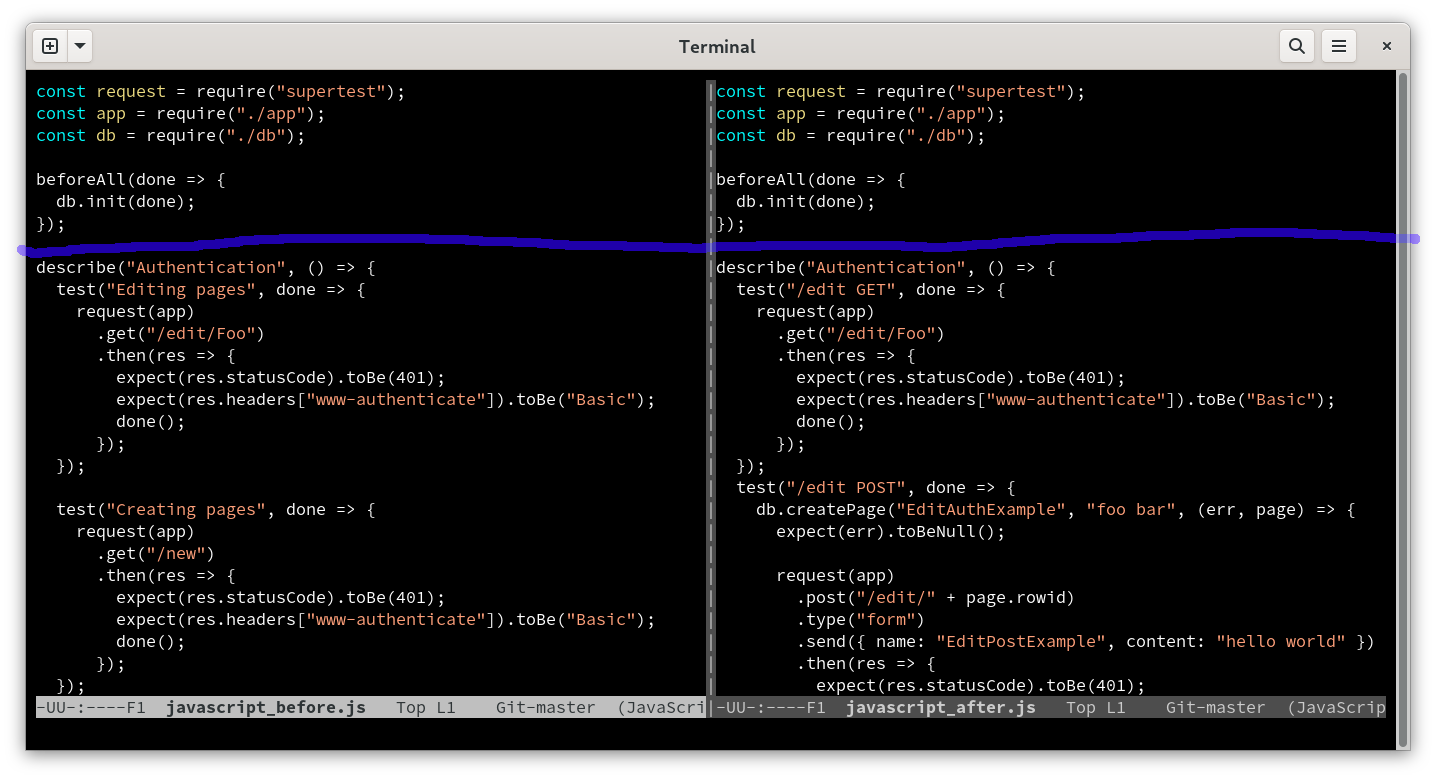
(GNU Diff has a similar feature with its horizon-lines option, although its performance is much better in general.)
Due to the sheer size of the graph (several million vertices), the biggest performance bottleneck is vertex construction. I explored better route finding algorithms (e.g. A*) but I didn’t see much improvement. My current solution is to construct the graph lazily, so few vertices are constructed.
Even with this, difftastic sometimes struggles with performance. I’ve profiled and optimised everything I can think of (using Rust really helped here). If the graph is just too big, difftastic falls back to a conventional line-oriented diff.
What About Nesting?
When incrementing positions during graph traversal, I needed to be careful with entering and leaving delimiters.
;; Before
(x y)
;; After
(x) y
The desired result here is
(x y)
and
(x) y.
When the s-expression position is on a delimiter, difftastic can either consider the delimiter novel, or unchanged. This is similar to the s-expression atom case.
START
+---------------------------+
| Left: (x y) Right: (x) y |
| ^ ^ |
+---------------------------+
/ | \
Novel delimiter L / | \ Novel delimiter R
v | v
+---------------------------+ | +---------------------------+
| Left: (x y) Right: (x) y | | | Left: (x y) Right: (x) y |
| ^ ^ | | | ^ ^ |
+---------------------------+ | +---------------------------+
|
| Unchanged delimiters
v
+---------------------------+
| Left: (x y) Right: (x) y |
| ^ ^ |
+---------------------------+
What happens when the position is at the end of the list? If difftastic entered the delimiters together (‘unchanged delimiter’), it must exit them together. This requires both s-expressions positions to point to the exit delimiter.
If the delimiters were entered separately (‘novel delimiter’), then the delimiters can be exited separately too.
+---------------------------+
| Left: (x y) Right: (x) y |
| ^ ^ |
+---------------------------+
/ \
Novel node L / \ Exit delimiter R
v v
+---------------------------+ +---------------------------+
| Left: (x y) Right: (x) y | | Left: (x y) Right: (x) y |
| ^ ^ | | ^ ^ |
+---------------------------+ +---------------------------+
The ‘exit delimiter right’ edge is only allowed if the delimiter was also entered with ‘novel delimiter right’.
This means that graph vertices are really a tuple of three items: (left-hand side position, right-hand side position, list_of_parents_to_exit_together).
This exponentially increases the size of the graph, O(2N) where N is the highest list nesting level in either input.
I solved this by only considering at most two graph vertices for each position pair. I always find a route this way (there exists a route to the end vertex from every other vertex) but it is not necessarily the shortest. In practice this seems to explore enough of the graph that the results are consistently great.
Building The Interface
Phew! After wrestling with diffing algorithms for some time, I thought building the UI would be straightforward. I was wrong.
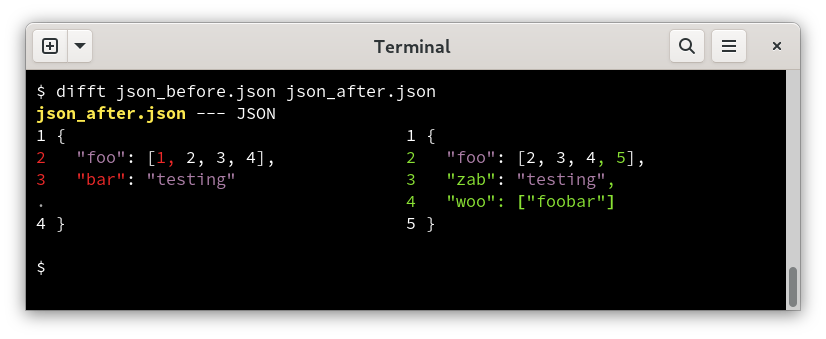
Difftastic knows which s-expression nodes are unchanged. It completely ignores whitespace.
However, there is no guarantee that there are any lines in common between the two files. It’s also possible that a line in the first file might have matches in zero, one or many lines in the second file.
The display logic iterates through all the matched lines, and tries to align as many as possible. It uses a two-column display by default, so you can reformat the entire file and it will still produce a sensible output.
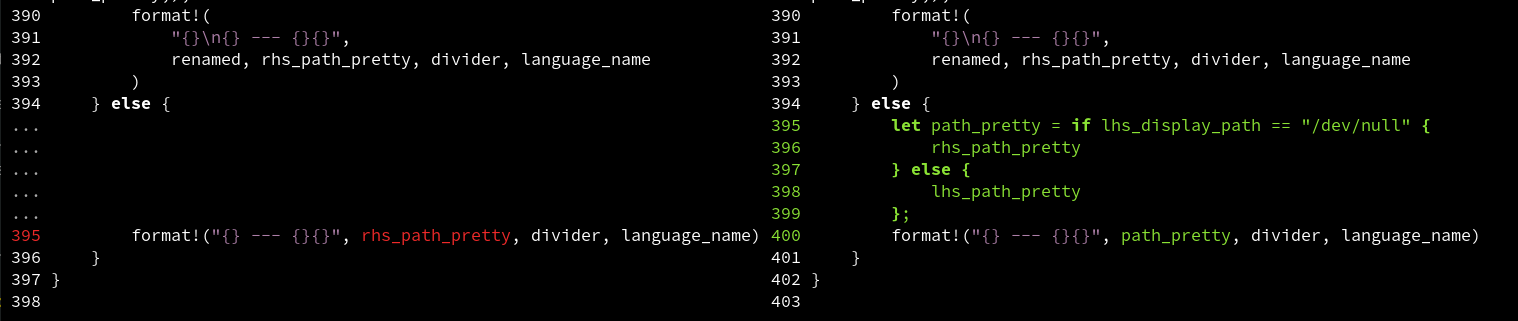
Working on diff UIs has made me realise how bad the traditional diff display is.
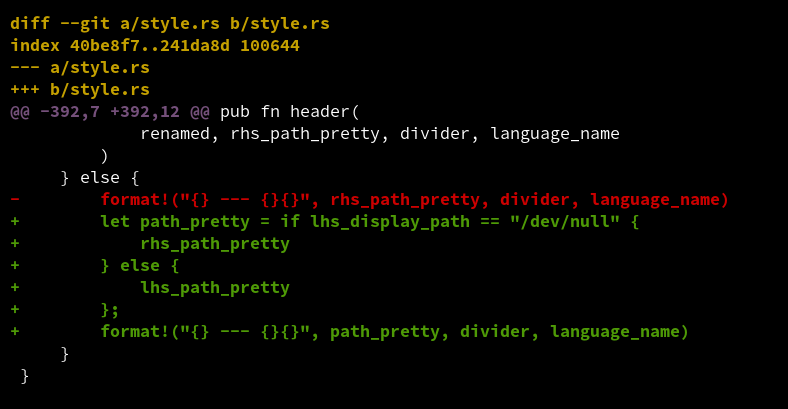
The header @@ -392,7 +392,12 @@ means that the diff starts at
line 392. The user is forced to count lines to work out that the change
itself is on line 395!
Dogfooding
Eventually I added the ability to use difftastic with git or mercurial. This was an exceptional way to find bugs and see how well the design works in practice.
This exposed a bunch of subtle issues with structural diffing.
;; Before
(foo (bar))
;; After
(foo (novel) (bar))
Diff algorithms are described in the literature as “finding a minimal edit script”, where the edit script is the additions/removals required to turn the input file into the output file.
In this example, (foo (novel)
(bar)) would be a totally
valid, minimal diff. It’s adding the symbol novel and adding one
pair of parentheses.
This isn’t what the user wants though. They’d rather see (foo (novel) (bar))
even though it’s equally minimal.
I solved this by adjusting the graph edge cost model to produce nicer results. I also added a secondary pass on the diff result to check for more aesthetically pleasing results with the same edge cost.
(I encountered several more cases that structural diffs struggle with, see the Tricky Cases page in the manual for more details.)
Future Work
Difftastic is fantastic when it works, and I use it daily. It’s still not perfect though.
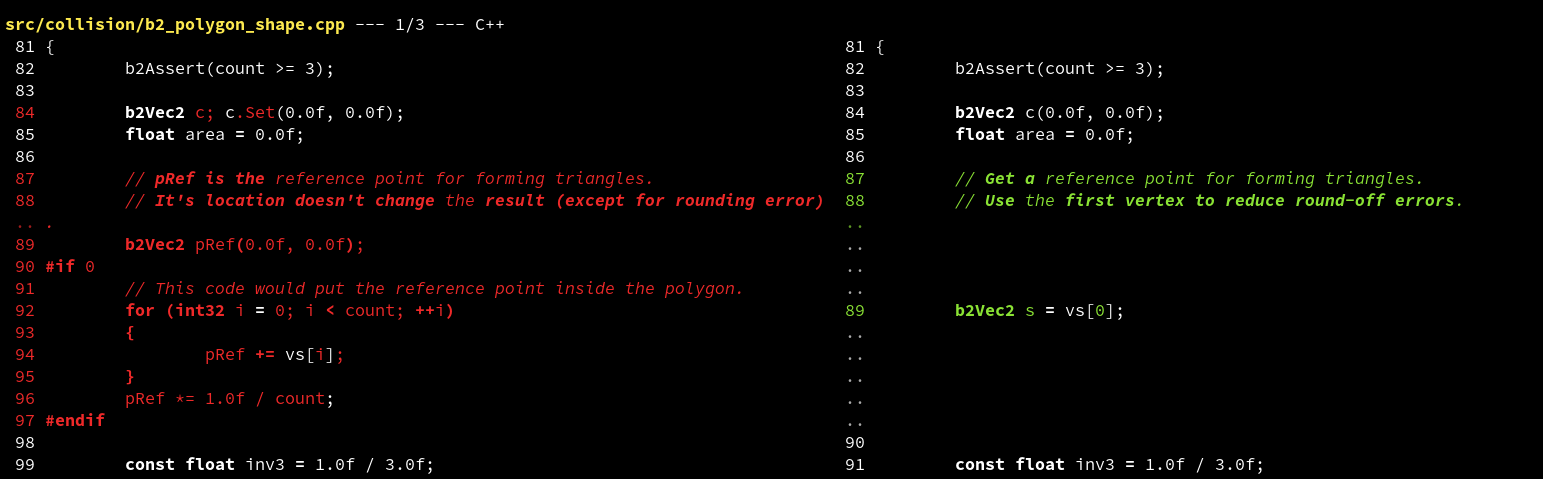
Difftastic has some complicated failure modes. Changing large string literals is a challenge (syntactically they’re single atoms, but users sometimes want a word-level diff).

The minimal diff isn’t always helpful either. Sometimes difftastic goes too far.
Closing Thoughts
I had no idea what I was getting into when I started working on this.
I’d been wondering why this type of tool is so rare. Now I know: it’s extremely challenging to build. Despite its limitations, I’m surprised at how often it works fantastically.
Difftastic is OSS under a MIT license, so I hope it enables more diff tools that can understand structure. If you’re feeling brave, you can even try it yourself!